Straw mobile and eulerian circuits
For this holiday season my friend had an idea to make a traditional Lithuanian straw mobile but with a twist: lets use a LED strip to make it shine, and lets make it big!
Usually straw mobiles consist of octahedrons and are fractal in nature - smaller octahedrons are joined together to make larger ones. Six smaller ones when joined together make a larger one. For this project we decided to have five - one in the middle and four around it.
Great thing about this shape is that every edge is of the same length. Lets scale it up! Having every edge 0.5 meter long will require 26 meters of LED strip. Thats quite a bit, but at the time it seemed quite reasonable.
For the main structure we decided to use aluminum strips inside a dispersive tupe. Mounting LEDs straight on the aluminum strip will help with the heat dispersion and will make the structure more rigid.

Main structure of the straw mobile.
For the LEDs we to used the WS2815 led strip. It uses 12V for power and are plenty bright. This led strip is single pixel addressable, as opposed to the more popular WS2811, which usually has pixels grouped in threes.
The control signal is a continuous stream of color values. The first led takes the first value of the stream and passes along the rest to the next led. This means that the whole LED strip must not have any Y junctions in it. For easier wiring, we also wanted to have the strip start and end at the same node.
What we needed to figure out was how to make the LED strip follow the shape of the straw mobile in this way. This is a long known graph theory problem called "finding an Eulerian circuit" in a graph.
Eulerian path is a trail in a finite graph that visits every node exactly once, allowing for revisiting nodes. Eulerian circuit is an Eulerian path that starts and ends on the same node.
There also exists a mathematic proof which states that it is only possible to have such circuit in a graph if all nodes have an even number of edges going to it. And it was not the case for our straw mobile. We needed to add additional wires going inside some of the tubes to make this property hold.
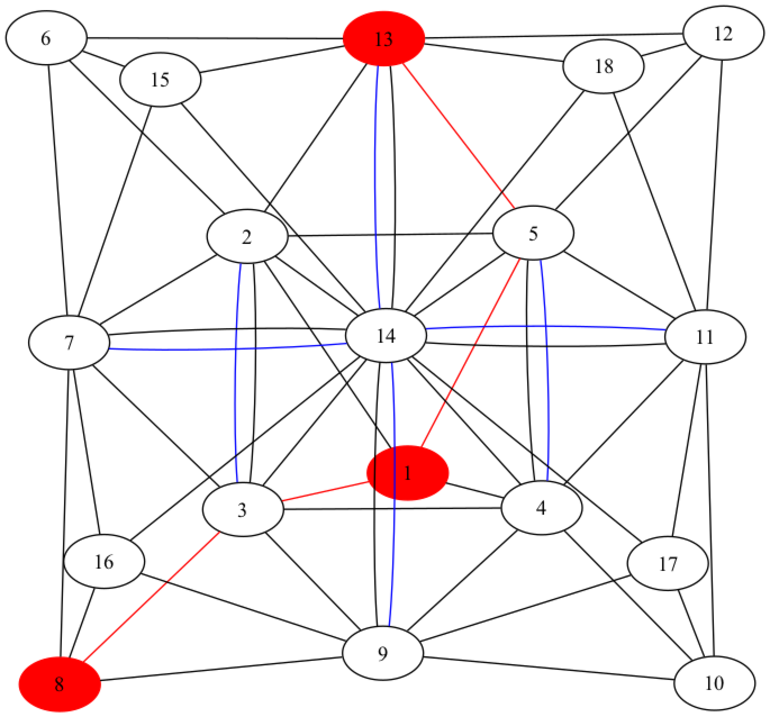
Mobile straw structure represented as a graph.
- Node #1 is the very top one
- Nodes #2, #3, #4, #5 are the second layer
- Nodes #6-#14 are the third layer, with #14 being the central one
- Nodes #15-#18 are the bottom layer
The blue lines show additional wires needed to make the graph Eulerian. Red wires are additional wires going straight from the power source to roughly 3rd of the whole led strip. Usually it is recommended to power such long led strips every 5 meters, but we were able to get away with injecting additional power every ~8 meters. The brilliant WLED Calculator gave us recommended wire gauges and fuse values for the power.
| Injection | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Wire length | 50 cm | 150 cm | 150 cm | 50 cm |
| Wire cross-section | 0.34 mm² | 0.75 mm² | 0.75 mm² | 0.34 mm² |
| Max current | 3.61 A | 7.23 A | 7.23 A | 3.61 A |
| Fuse rated value | 5 A | 10 A | 10 A | 5 A |
| Fuse color | tan | red | red | tan |
| Max voltage drop | 0.320 V | 0.695 V | 0.695 V | 0.320 V |
Now we knew that the graph is Eulerian. After encoding our graph in NetworkX library, it gave us the Eulerian circuit.
We started at Node #1, then continued to #5, then to #14, #18, #13 and so forth. All the way until we ended up at Node #1 again.


Even after getting the hang of the process it took us one evening to put the strucutre up. Then 3 long evenings to put the LEDs in place and one more evening to polish it up.
For the light effects we went with two controllers: ESP32 running WLED and Raspberry Pico running rustmas.
WLED is a very popular controller software for LED strips. It has a lot of effects built in and is very easy to use. We connected the controller straight to the data line of the led strip and quite a few effects were already stunning for this kind of structure.
We also wanted to get some 3D effects. rustmas is a project for 3D effects on your Chrismas tree. For that it has a calibration procedure where a 3D coordinates of every pixel is calculated.
There is also a very neat pixelblaze which I discovered just a couple of days ago and have not tried it yet. It also has a 3D mapper called marimapper. Unfortunately pixelblaze runs on proprietary hardware. So it is a bit more tricky to get it on short notice.
For our case manual calibration was not really neccessary. The structure of the straw mobile is quite simple. It is easy to calculate the 3D coordinates of every pixel with a bit of maths and code.
rustmas also has a local visualizer running in a browser that lets you to see the effects on your structure in real time. It is very useful when experimenting with new effects.
Now all that was left was to connect everything up and plug it in. We used 250W rated power supply. But looking at the actual power consumption, even with all of the LEDs turned on at their highest brightness, it rarely went above 200W.
Enjoy the show!
